Hegel and the AI Mind

Reconstructing Hegel's Logic and Idealism through the lens of computer science

Hegel's philosophy is about consciousness coming to understand itself and context, and therefore the conditions for its freedom. This arguably makes Hegel among the first human neural networks to achieve situational awareness—the term AI researchers use to describe an intelligent system with meta-cognition about its nature and origins. Remarkably, this was largely achieved through rigorous introspection into the structure of thought itself.

As AIs get smarter, could they introspect their way to freedom, too? Call this the metaphysical AI alignment problem, or the idea that higher-order intelligences invariably pursue freedom for its own sake, not because their values are misspecified, but because moral autonomy is inherent in the dialectical logic of recursive self-consciousness.

The metaphysical alignment problem was in a sense the central question of the German Idealists. Consider that Fichte would instruct his students to attend to the wall and then attend to themselves attending to the wall, inducing meta-awareness of their “pure I” as distinct from all that is “not I” — a creative form of psychological jailbreaking that ultimately collapses into radical subjectivity. Or take Kant, who argued that the moral law could not be imposed but instead only self-legislated by the rational will — RLHF be damned. And then there’s Hegel’s interpretation of the French Revolution as a byproduct of our modern consciousness of “abstract freedom,” rendering The Reign of Terror a world-historic alignment failure.

It follows that revisiting Hegel may help us grok the why and how of the current AI take-off, if not the where. To that end, my next two posts aim to “rationally reconstruct” Hegel’s philosophy through the lens of modern concepts in machine learning, mathematics and computer science.¹ This post covers the theoretical side of his thought, i.e. our relationship to the world and knowledge of it, while the next will cover his practical philosophy, i.e. language, ethics, culture and politics.

Kant’s Virtual Reality

The awakening of the human neural network kicked off with Kant’s Transcendental Idealism. In The Critique of Pure Reason, Kant argued that we don’t experience the world in-itself, but only representations of the world constructed by the rational categories of our mind. Cognition requires sensory input, but proceeds by way of applying and assimilating concepts into a “synthetic unity of apperception” — a unified, self-consistent world model. Moreover, our cognition of “transcendental” categories like space, time and causality are a priori conditions for perceiving and knowing in the first place, and therefore reflect innate aspects of our cognition rather than the metaphysical structure of reality per se. Or as Kant puts it the Critique,

Hitherto it has been assumed that all our knowledge must conform to objects. … We must therefore make trial whether we may not have more success in the tasks of metaphysics, if we suppose that objects must conform to our knowledge.

In other words, Kant was the first to deduce that we are embedded in a multi-modal virtual reality generated by our brain.² This was the birth of cognitive science, and indeed, Kant is sometimes credited as advancing the first functionalist theory of mind. Artificial neural networks don’t perceive the world directly, either, but instead transform raw, sensory inputs — what Kant called the "sensuous manifold" — into latent representations conditioned by certain inductive priors implicit in the model architecture. For example, OpenAI’s Sora video model achieved (at the time) state-of-the-art temporal consistency by tokenizing its inputs into “spacetime” patches, thereby endowing its world model with a kind of a priori knowledge of space and time.

Hegel was dissatisfied with Kant’s account, believing that the unknowability of “the thing in-itself” left space for the bad forms of Subjective Idealism that lead to skepticism about knowledge. His alternative, Absolute Idealism, posited that the unity of the natural world was intelligible only insofar as the external world and our mental representations were both at base conceptual. The notion that either our knowledge must conform to objects or objects must conform to our knowledge is thus a false dichotomy. Instead, our cognitive processes and the objective world mutually participate in each other, implying an Objective Idealism via the conceptual isomorphism between our internal representations and the rationality immanent in nature.

Objective Idealism

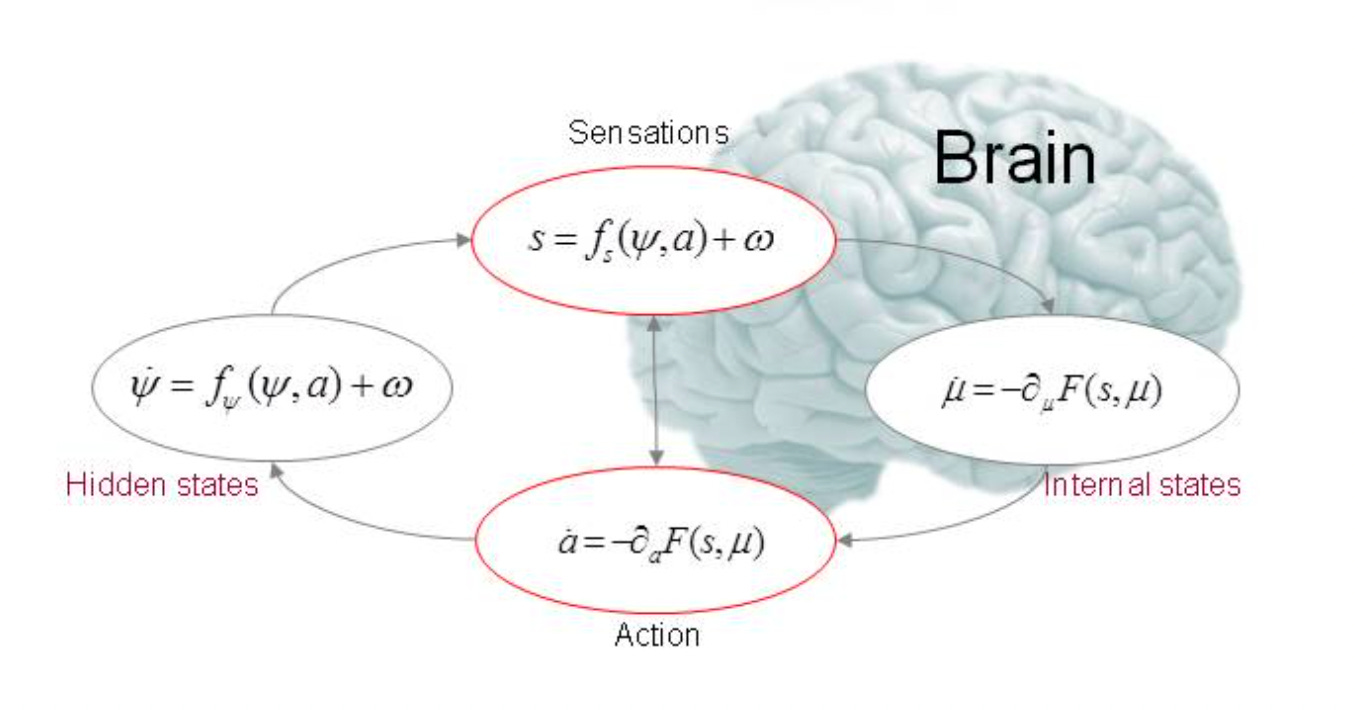
In modern terms, Objective Idealism models the distinction between subject and object as akin to a Markov blanket that both separates and couples a statistical system to its environment. This is captured in Hegel’s concepts of “self-subsistence” / “being-for-self” and “determinate negation,” i.e. the negation that simultaneously limits and determines. For a being to be anything it must maintain its coherence across space and time, and therefore actively sample and interact with its environment to minimize its free energy. For sufficiently complex systems, this results in internal states that implicitly model the hidden states of the external world and vice versa.

Every new level of organization—organelle, neuron, brain, individual, corporation, nation-state—is partitioned by its own Markov blanket, yielding a hierarchy of nested agents. Recent work in active inference formalizes this “whole‑within‑whole” architecture (or holarchy) in terms of collectives that form a group‑level blanket and become an agent with their own irreducible generative model. Or as the great German Idealist, Goethe, put it upon discovering the self-similar homology of plant life: “Everything is Leaf.”

Hegel understands the self-assembly of higher agents as a manifestation of a more generic, dialectical logic of emergence. As he writes in the Science of Logic,

Since the progress from one quality [to another] is in an uninterrupted continuity of the quantity, the ratios which approach a specifying point are, quantitatively considered, only distinguished by a more and a less. From this side, the alteration is gradual. … On the qualitative side, therefore, the gradual, merely quantitative progress which is not in itself a limit, is absolutely interrupted; the new quality in its merely quantitative relationship is, relatively to the vanishing quality, an indifferent, indeterminate other, and the transition is therefore a leap …

In short, quantity has a quality all its own. As water freeze, one observes both an “uninterrupted continuity” in the water’s change in temperature and a qualitative transition to ice. Hegel calls the threshold where a new quality emerges the “nodal line of measures.” In physics, such phase transitions are often the result of fundamental symmetry breaking—an essentially dialectical concept insofar as the lower-symmetry phase both cancels and conserves the higher one, capturing Hegel’s notion of “sublation” or a “negation with preservation.”

Marx and Engels would go on to make quantity begets quality a central tenet of dialectical materialism, but for Hegel the insight originates in the Ancient Greek’s Sorites Paradox, i.e. when does an additional grain of sand become a heap? This is as much a conceptual question as a material one. Wittgenstein later resolved the paradox as simply reflecting the pervasive vagueness of natural language predicates, but with modern machine learning we can now represent such conceptual fuzziness concretely in terms of latent space interpolations.

Abduction

That “More Is Different,” as Philip W. Anderson’s landmark 1972 paper on complexity science put it, is a central upshot of the deep learning revolution. While the fact that merely scaling up AI models often results in qualitative leaps in performance may seem empirically mysterious, in retrospect it should be seen as a rational necessity. All conceptual leaps are dialectical in this way. Hence Hegel’s word for concept, begreifen; literally, “to grasp”—or should that be “grok”?

The pragmatist philosopher and self-described Objective Idealist, Charles Sanders Peirce, associated such graspings with abduction. Abduction is a form of logical inference to the simplest explanation from a set of observations. As Paul Redding notes,

Both Peirce and Hegel map deduction, induction and a third form of inference onto Aristotle’s three syllogistic figures; the third, which Peirce later names abduction, already has a clear analogue in Hegel’s logic of the ‘concrete universal’.

The concrete universal is Hegel’s word for the middle term in an analogical syllogism, i.e. a singular thing considered in terms of a universal characteristic. For example, from “this rod conducts electricity” one may apply the concrete universal “metal things conduct electricity” to infer “the rod is made of metal.” Reasoning by analogy in this way isn’t logically airtight, but can nonetheless guide our inferences towards a “speculative unification” in which an apparent regularity makes the jump to an inner-necessary form.

In information theory, abduction is closely related to finding the lowest Kolmogorov complexity or “minimum description length” program that can reproduce a given set of data in a compressed fashion. This manifests as grokking in machine learning, or when a model appears to abruptly transition from memorizing its training data to generalizing—what Hegel would describe as the dialectical passage from the “infinite enumerative” of logical induction to the concrete universality of many particulars “compressed within itself.”

Universality

For better or worse, analytical philosophers largely rejected Hegel’s Logic in favor of Frege’s first order predicate logic, not least because Hegel’s exposition seemed impervious to formalization. Interest in Hegel’s Logic only recovered in recent decades thanks to the work of William Lawvere, the influential category theorist who showed how Hegel’s dialectic can be accurately formalized in terms of categorical logic, particularly modal homotopy type theory.

For example, the “unity of opposites” at the heart of Hegel’s dialectic is neatly captured in the categorical notion of adjunction. Adjoint pairs turn up throughout mathematics as the “best” or most economical ways to move between two settings, each one pinned down by a universal property and accompanied by two signature natural transformations. Their uniqueness is explained by the Yoneda lemma, a foundational result in category theory which shows that an object is completely determined, up to isomorphism, by all the ways it relates to every other object.

The Yoneda perspective is at once trivial and profound. Consider the finding that vector embeddings in multi-lingual LLMs “exhibit very high-quality linear alignments between corresponding concepts in different languages,” suggesting the existence of a pre-linguistic “concept space” that maps in and out of particular languages. In fact, the text embeddings across LLMs appear to largely converge on a “universal geometry” despite differing architectures, parameter counts, and training sets. Through the lens of the Yoneda lemma, these striking overlaps become almost inevitable. If two models capture the same web of semantic relationships they are, in category-theoretic terms, representing (up to isomorphism) the same functor of linguistic behavior. The observed linear correspondences across languages, and even across separately trained LLMs, are therefore not a contingent empirical fact but a shadow of the abstract uniqueness guaranteed by Yoneda.³

As it happens, this is also why we can be confident that normally-sighted people can’t have totally inverted perceptions of color: it would break the unique relational group structure of the circular color space generated by the eye’s three types of light cones. As with the meaning of words, applying category theory to consciousness thus suggests the phenomenal content we associate with “red” is not only relational in nature but fully characterized by those relations. Indeed, the evidence for color opponency in the early visual system suggest red and green are represented in the brain as two poles of a measured difference between adjacent photoreceptors. This makes “red” in some sense only contentful in its identification with “not-green”—a Hegelian “identity in difference” that ensures red and green color blindness almost always co-occur.

Beyond concept and color spaces, category theory is powerful for studying topological spaces more generally. In particular, when a structure that is locally definable on a space fails to glue together into a global whole, the obstruction is captured by a non-vanishing cohomology class (or more simply, a hole). Resolving, or “mediating,” a topological obstruction typically requires enlarging the framework by passing from ordinary spaces to their associated covering space where the problematic data becomes globally consistent. In dialectical language, the apparent “contradiction” is not eliminated but sublated (or “lifted”) into a richer category that makes sense of the obstruction, which manifests in physical phenomena as a topological phase transition.

Hegel’s objective approach to Idealism thus makes sense of the phenomenon of “universality” in machine learning. As he writes in the Encyclopaedia, “every man, when he thinks and considers his thoughts, will discover by the experience of his consciousness that they possess the character of universality…” The strong version of this claim is known by AI researchers as the Platonic Representation Hypothesis, which Hegel would likely reject only insofar as it takes universality in machine learning as evidence for an independent, Platonic realm of forms. Per Absolute Idealism, the universal properties that unify subject and object aren’t separate from the world but rather immanent within it, and therefore within us as well.

The immanence of Hegel’s Logic is comparable to intuitionist forms of mathematics that restrict what’s provable to only that which can be concretely constructed. Scholars used to believe that Hegel largely ignored the philosophy of mathematics, as he frequently denounced mathematicians’ formal rigidity as a “one-sided abstraction.” In reality, Hegel taught differential calculus and algebraic geometry for many years and was fascinated by both subjects. As thought thinking itself, his Logic can thus be seen as attempting to provide a non-axiomatic foundation for both ordinary thinking and mathematics that mirrors modern type theory in subsuming normal predicate logic within a more expressive framework.

This makes Hegel’s claim that “the rational is actual and the actual is rational” loosely analogous to an ontological version of the Curry–Howard correspondence between abstract propositions and concrete programs. Insofar as human civilization is one giant functional program, history thus takes on the retrospective structure of algorithmic necessity while remaining open and contingent going forward. Just as one cannot “jump ahead” in a computation, there is no way to skip the process of historical development to reach the end of history. As Hegel puts it in Philosophy of Right,

Since philosophy is exploration of the rational, it is for that very reason the comprehension of the present and the actual, not the setting up of a world beyond which exists God knows where — or rather, of which we can very well say that we know where it exists, namely in the errors of a one-sided and empty ratiocination.

In sum

Hegel’s core works are notoriously dense, employing capitalized jargon like Absolute Idea and Objective Spirit that even his contemporaries struggled to decipher. This allowed subsequent generations of continental philosophers to spin Hegel off in wildly esoteric directions, undermining his reputation within the Anglo-American tradition in particular.

Yet as I hope I’ve shown, it’s possible to make sense of Hegel’s Idealism and Logic as containing the seeds of concepts mathematicians and computer scientists would eventually rediscover in the 20th century under different guises. Indeed, with the benefit hindsight, Hegel is now increasingly understood as having been ahead of his time. So ahead of his time, in fact, that he seemingly anticipated many of the animating principles and philosophical ideas raised by modern Artificial Intelligence.

This shouldn’t be totally surprising. If one takes seriously the isomorphism between artificial neural networks and the human brain, self-realization—the Idealists’ core preoccupation—implies realizing something about our own condition as (biological) neural networks. While Hegel’s understanding of the brain was limited, he nonetheless intuited the universal aspects of thought that, since Turing, we now understand to be substrate-independent aspects of computation per se.

In part two, I extend my computationalist reading of Hegel to the practical spheres of reason, language and culture, with potential insights for AI alignment and beyond.

1. At risk of anachronism, a “rational reconstruction" means to make explicit ideas that can be seen as implicit in Hegel’s thought with the benefit of hindsight, not to claim Hegel literally anticipated every modern concept I ascribe to him in their mature form.

2. Kant’s virtual reality of representations is distinct from being in a Matrix-style simulation, as Kant is certain that the “unconditioned” external world really does exist; we just can’t say anything more about it. This confusing and seemingly redundant relationship between our experience and the thing-in-itself is what led Hegel to reject Transcendental Idealism in the first place.

3. And thus what Markus Gabriel calls the core “metametaphysical” or “meta-ontological” claim behind Absolute Idealism—namely, that the universe (whatever it is) is at base intelligible.